GNUPLOT-3.7 demo: prob2.dem
#
# $Id: prob2.dem,v 1.3 1994/03/30 01:28:45 alex Exp $
#
# Demo Statistical Approximations version 1.1
#
# Permission granted to distribute freely for non-commercial purposes only
#
# Copyright (c) 1991, Jos van der Woude, jvdwoude@hut.nl
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 " Statistical Approximations, version 1.1"
pause 0 ""
pause 0 " Copyright (c) 1991, 1992, Jos van de Woude, jvdwoude@hut.nl"
pause 0 ""
pause 0 ""
pause 0 " Permission granted to distribute freely for non-commercial purposes only"
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 ""
pause 0 " NOTE: contains 10 plots and consequently takes some time to run"
pause 0 " Press Ctrl-C to exit right now"
pause 0 ""
pause -1 " Press Return to start demo ..."
load "stat.inc"
# Binomial PDF using normal approximation
n = 25; p = 0.15
mu = n * p
sigma = sqrt(n * p * (1.0 - p))
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
ymax = 1.1 * binom(mu) #mode of binomial PDF used
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil(sigma), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
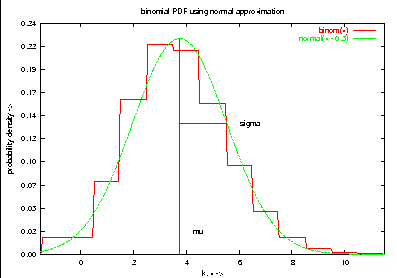
set title "binomial PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot binom(x), normal(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Binomial PDF using poisson approximation
n = 50; p = 0.1
mu = n * p
sigma = sqrt(mu)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
ymax = 1.1 * binom(mu) #mode of binomial PDF used
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil(sigma), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "binomial PDF using poisson approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot binom(x), poisson(x)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Binomial PDF using poisson approximation
n = 50; p = 0.1
mu = n * p
sigma = sqrt(mu)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
ymax = 1.1 * binom(mu) #mode of binomial PDF used
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil(sigma), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
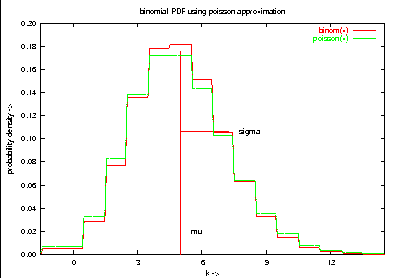
set title "binomial PDF using poisson approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot binom(x), poisson(x)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Geometric PDF using gamma approximation
p = 0.3
mu = (1.0 - p) / p
sigma = sqrt(mu / p)
lambda = p
rho = 1.0 - p
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * p
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "geometric PDF using gamma approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, g(mu) nohead
set arrow from mu + 0.5, g(mu + sigma) \
to mu + 0.5 + sigma, g(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, g(mu + sigma)
plot geometric(x), g(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Geometric PDF using gamma approximation
p = 0.3
mu = (1.0 - p) / p
sigma = sqrt(mu / p)
lambda = p
rho = 1.0 - p
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * p
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
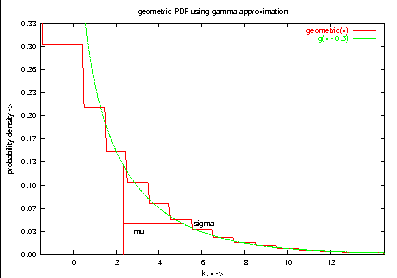
set title "geometric PDF using gamma approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, g(mu) nohead
set arrow from mu + 0.5, g(mu + sigma) \
to mu + 0.5 + sigma, g(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, g(mu + sigma)
plot geometric(x), g(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Geometric PDF using normal approximation
p = 0.3
mu = (1.0 - p) / p
sigma = sqrt(mu / p)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * p
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "geometric PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot geometric(x), normal(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Geometric PDF using normal approximation
p = 0.3
mu = (1.0 - p) / p
sigma = sqrt(mu / p)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * p
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
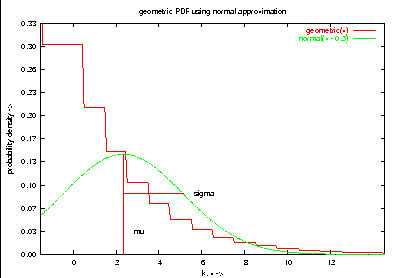
set title "geometric PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot geometric(x), normal(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Hypergeometric PDF using binomial approximation
nn = 75; mm = 25; n = 10
p = real(mm) / nn
mu = n * p
sigma = sqrt(real(nn - n) / (nn - 1.0) * n * p * (1.0 - p))
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * hypgeo(mu) #mode of binom PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
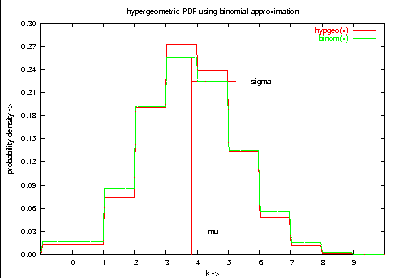
set title "hypergeometric PDF using binomial approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, binom(mu) nohead
set arrow from mu + 0.5, binom(mu + sigma) \
to mu + 0.5 + sigma, binom(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, binom(mu + sigma)
plot hypgeo(x), binom(x)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Hypergeometric PDF using binomial approximation
nn = 75; mm = 25; n = 10
p = real(mm) / nn
mu = n * p
sigma = sqrt(real(nn - n) / (nn - 1.0) * n * p * (1.0 - p))
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * hypgeo(mu) #mode of binom PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "hypergeometric PDF using binomial approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, binom(mu) nohead
set arrow from mu + 0.5, binom(mu + sigma) \
to mu + 0.5 + sigma, binom(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, binom(mu + sigma)
plot hypgeo(x), binom(x)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Hypergeometric PDF using normal approximation
nn = 75; mm = 25; n = 10
p = real(mm) / nn
mu = n * p
sigma = sqrt(real(nn - n) / (nn - 1.0) * n * p * (1.0 - p))
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * hypgeo(mu) #mode of binom PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "hypergeometric PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot hypgeo(x), normal(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Hypergeometric PDF using normal approximation
nn = 75; mm = 25; n = 10
p = real(mm) / nn
mu = n * p
sigma = sqrt(real(nn - n) / (nn - 1.0) * n * p * (1.0 - p))
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * hypgeo(mu) #mode of binom PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
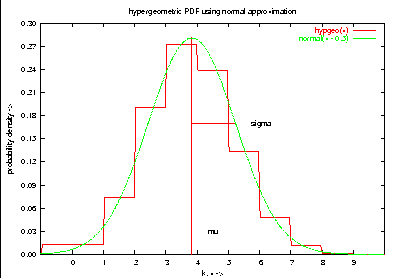
set title "hypergeometric PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot hypgeo(x), normal(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Negative binomial PDF using gamma approximation
r = 8; p = 0.6
mu = r * (1.0 - p) / p
sigma = sqrt(mu / p)
lambda = p
rho = r * (1.0 - p)
xmin = int(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = int(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * g((rho - 1) / lambda) #mode of gamma PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "negative binomial PDF using gamma approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, g(mu) nohead
set arrow from mu + 0.5, g(mu + sigma) \
to mu + 0.5 + sigma, g(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, g(mu + sigma)
plot negbin(x), g(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Negative binomial PDF using gamma approximation
r = 8; p = 0.6
mu = r * (1.0 - p) / p
sigma = sqrt(mu / p)
lambda = p
rho = r * (1.0 - p)
xmin = int(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = int(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * g((rho - 1) / lambda) #mode of gamma PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
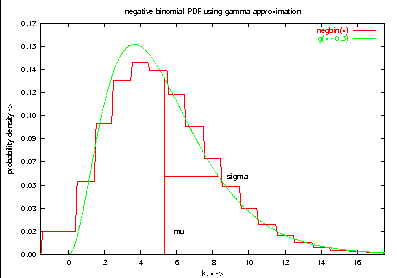
set title "negative binomial PDF using gamma approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, g(mu) nohead
set arrow from mu + 0.5, g(mu + sigma) \
to mu + 0.5 + sigma, g(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, g(mu + sigma)
plot negbin(x), g(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Negative binomial PDF using normal approximation
r = 8; p = 0.4
mu = r * (1.0 - p) / p
sigma = sqrt(mu / p)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * negbin(mu - 1/p) #mode of gamma PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "negative binomial PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot negbin(x), normal(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Negative binomial PDF using normal approximation
r = 8; p = 0.4
mu = r * (1.0 - p) / p
sigma = sqrt(mu / p)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * negbin(mu - 1/p) #mode of gamma PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin + 0.499, ceil((xmax - xmin)/ 10.0), xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
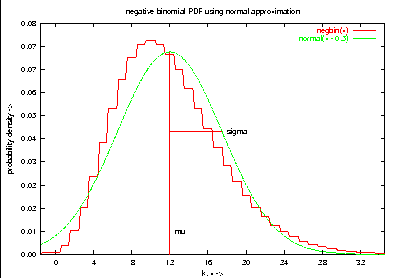
set title "negative binomial PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot negbin(x), normal(x - 0.5)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Normal PDF using logistic approximation
mu = 1.0; sigma = 1.5
a = mu
lambda = pi / (sqrt(3.0) * sigma)
xmin = mu - 4.0 * sigma
xmax = mu + 4.0 * sigma
ymax = 1.1 * logistic(mu) #mode of logistic PDF used
set key
set nozeroaxis
set xrange [xmin: xmax]
set yrange [0 : ymax]
set xlabel "x ->"
set ylabel "probability density ->"
set xtics xmin, (xmax - xmin)/ 10.0, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%.1f"
set format y "%.2f"
set sample 200
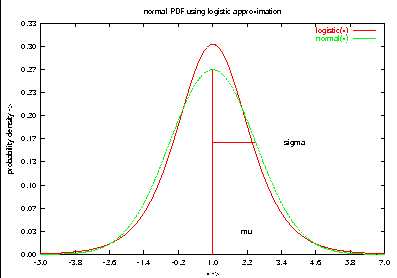
set title "normal PDF using logistic approximation"
set arrow from mu,0 to mu, normal(mu) nohead
set arrow from mu, normal(mu + sigma) \
to mu + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot logistic(x), normal(x)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Normal PDF using logistic approximation
mu = 1.0; sigma = 1.5
a = mu
lambda = pi / (sqrt(3.0) * sigma)
xmin = mu - 4.0 * sigma
xmax = mu + 4.0 * sigma
ymax = 1.1 * logistic(mu) #mode of logistic PDF used
set key
set nozeroaxis
set xrange [xmin: xmax]
set yrange [0 : ymax]
set xlabel "x ->"
set ylabel "probability density ->"
set xtics xmin, (xmax - xmin)/ 10.0, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%.1f"
set format y "%.2f"
set sample 200
set title "normal PDF using logistic approximation"
set arrow from mu,0 to mu, normal(mu) nohead
set arrow from mu, normal(mu + sigma) \
to mu + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot logistic(x), normal(x)
 pause -1 "Hit return to continue"
set noarrow
set nolabel
# Poisson PDF using normal approximation
mu = 5.0
sigma = sqrt(mu)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * poisson(mu) #mode of poisson PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
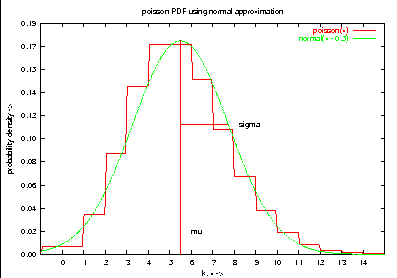
set title "poisson PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot poisson(x), normal(x - 0.5)
pause -1 "Hit return to continue"
set noarrow
set nolabel
# Poisson PDF using normal approximation
mu = 5.0
sigma = sqrt(mu)
xmin = floor(mu - 4.0 * sigma)
xmin = xmin < 0 ? 0 : xmin
xmax = ceil(mu + 4.0 * sigma)
xinc = ceil((xmax - xmin) / 10)
xinc = xinc > 1 ? xinc : 1
ymax = 1.1 * poisson(mu) #mode of poisson PDF used
set key
set nozeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x ->"
set ylabel "probability density ->"
set xtics xmin, xinc, xmax
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
set title "poisson PDF using normal approximation"
set arrow from mu + 0.5, 0 to mu + 0.5, normal(mu) nohead
set arrow from mu + 0.5, normal(mu + sigma) \
to mu + 0.5 + sigma, normal(mu + sigma) nohead
set label "mu" at mu + 1, ymax / 10
set label "sigma" at mu + 1 + sigma, normal(mu + sigma)
plot poisson(x), normal(x - 0.5)
 set noarrow
set nolabel
set noarrow
set nolabel



















